热门关键字: 激光共聚焦显微镜VSPI 工业视频显微镜WY-OL01 三目倒置金相显微镜WYJ-4XC-Ⅱ 三目倒置金相显微镜WYJ-4XC 恒信彩票
热门关键字: 激光共聚焦显微镜VSPI 工业视频显微镜WY-OL01 三目倒置金相显微镜WYJ-4XC-Ⅱ 三目倒置金相显微镜WYJ-4XC 恒信彩票
 精度高耐用High precision and durability
精度高耐用High precision and durability
恒信彩票采用进口核心零部件,显微镜精度高,产品性能稳定,经久耐用自然使用寿命长。
 智能 · 简便Intelligent and simple
智能 · 简便Intelligent and simple
微仪显微镜智能化程度高,优化人机界面设计,操作更简单。
 多重安全防护Multiple security protection
多重安全防护Multiple security protection
拥有多重安全防护设计措施,有效预防意外发生,确保实验应用的安全性。

 工业级设计Industrial Design
工业级设计Industrial Design
采用工业级美学设计理念,结构紧凑合理,占地小,外型线条流畅,有效提升实验室的整体美观度。
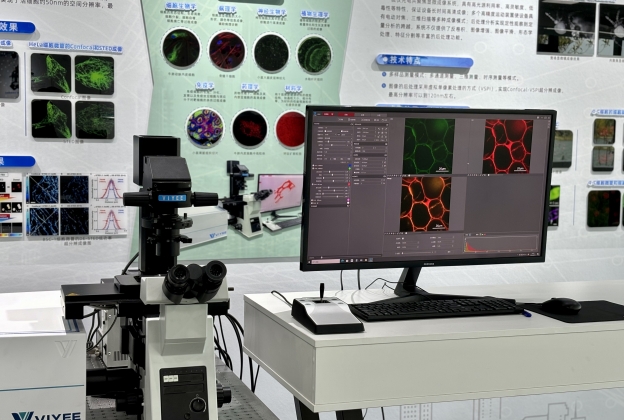
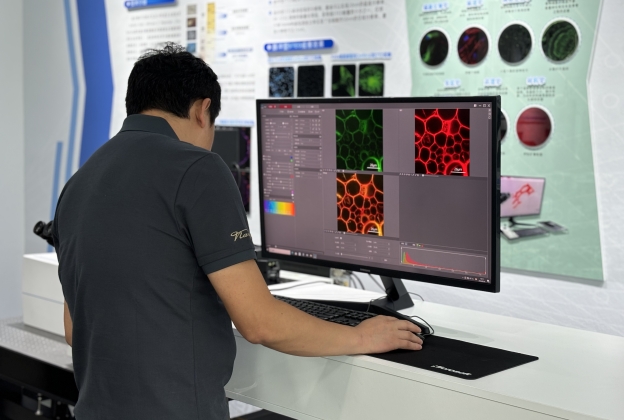
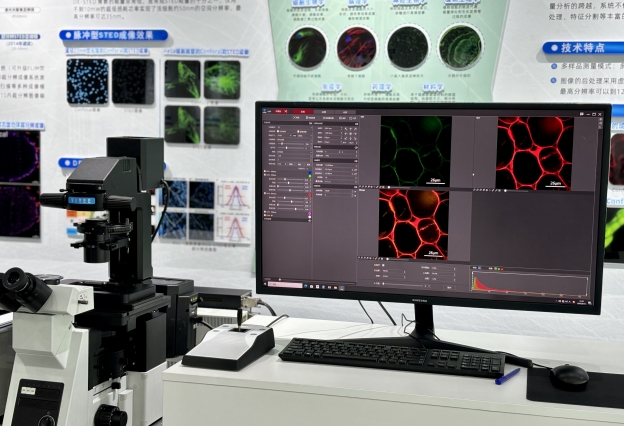
 激光共聚焦显微镜VSPI
激光共聚焦显微镜VSPI
 工业视频显微镜WY-OL01
工业视频显微镜WY-OL01
 三目倒置金相显微镜WYJ-4XC-Ⅱ
三目倒置金相显微镜WYJ-4XC-Ⅱ
 三目倒置金相显微镜WYJ-4XC
三目倒置金相显微镜WYJ-4XC
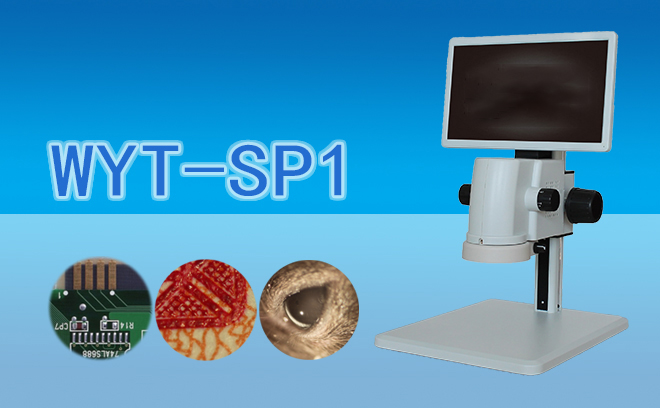 视频一体显微镜WYT-SP1
视频一体显微镜WYT-SP1
 大视野立体显微镜WYT-DP1
大视野立体显微镜WYT-DP1
 三目倒置金相显微镜V3910
三目倒置金相显微镜V3910
 三目倒置金相显微镜V3930
三目倒置金相显微镜V3930
 科研级三目生物显微镜WYS-08C
科研级三目生物显微镜WYS-08C
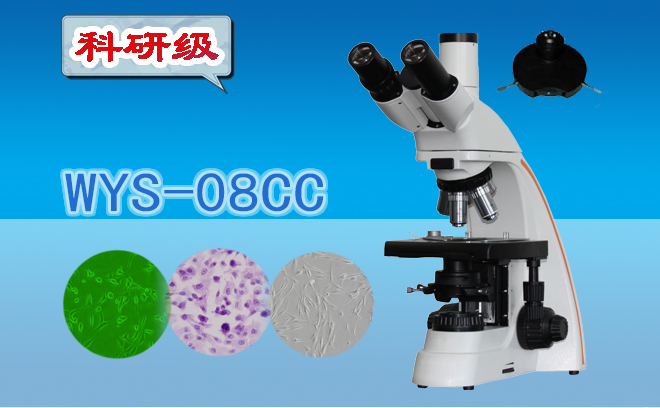 三目相衬显微镜WYS-08CC
三目相衬显微镜WYS-08CC
 三目暗视野显微镜WYS-11CA
三目暗视野显微镜WYS-11CA
 科研级三目荧光显微镜WYS-18CY
科研级三目荧光显微镜WYS-18CY
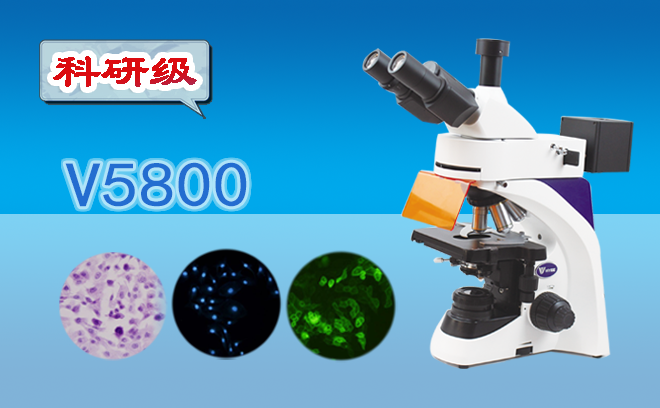 科研级三目荧光显微镜V5800
科研级三目荧光显微镜V5800
 三目连续变倍体视显微镜WYT-AT
三目连续变倍体视显微镜WYT-AT
 三目透反射金相显微镜WYJ-57C
三目透反射金相显微镜WYJ-57C
 三目金相显微镜V3800
三目金相显微镜V3800
 原子力显微镜(探头扫描式) WY- LS-AFM
原子力显微镜(探头扫描式) WY- LS-AFM
 原子力显微镜(平板扫描式) WY- LSCL-AFM
原子力显微镜(平板扫描式) WY- LSCL-AFM
 原子力显微镜(光学一体机) WY-Op-AFM
原子力显微镜(光学一体机) WY-Op-AFM
 原子力显微镜(教学型) WY-T-AFM
原子力显微镜(教学型) WY-T-AFM
 扫描隧道显微镜(教学型) WY-T-STM
扫描隧道显微镜(教学型) WY-T-STM
 原子力显微镜 WY-1000-AFM
原子力显微镜 WY-1000-AFM
 原子力显微镜 WY-6800-AFM
原子力显微镜 WY-6800-AFM
 三目生物显微镜V1600
三目生物显微镜V1600
 科研级三目生物显微镜V1800
科研级三目生物显微镜V1800
 三目生物显微镜V1500
三目生物显微镜V1500
 科研级三目生物显微镜V1700
科研级三目生物显微镜V1700
 科研级三目荧光显微镜WYS-18CY
科研级三目荧光显微镜WYS-18CY
 三目荧光显微镜WYS-13CY
三目荧光显微镜WYS-13CY
 倒置荧光显微镜WYS-37XBY
倒置荧光显微镜WYS-37XBY
 微仪仪器 Why choose Viyee Optics
微仪仪器 Why choose Viyee Optics  研产一体可靠质量保障自主研发、自主制造,实施全面品质管理。
研产一体可靠质量保障自主研发、自主制造,实施全面品质管理。
 研产一体可靠质量保障
研产一体可靠质量保障 自主研发、自主制造,实施全面品质管理。
自主研发、自主制造,实施全面品质管理。
 厂价直供高性价比之选微仪仪器实行从工厂直达用户的直供模式,原材为品牌厂家的一手货源,直接采购合理控制制造成本。
厂价直供高性价比之选微仪仪器实行从工厂直达用户的直供模式,原材为品牌厂家的一手货源,直接采购合理控制制造成本。
 厂价直供高性价比之选
厂价直供高性价比之选 微仪仪器实行从工厂直达用户的直供模式,原材为品牌厂家的一手货源,直接采购合理控制制造成本。
微仪仪器实行从工厂直达用户的直供模式,原材为品牌厂家的一手货源,直接采购合理控制制造成本。
 现货储备快速准时交付常规储备量为6000+台,批量订单可快至当天发货,长期与品牌物流公司签约合作,可提供门对门的配送服务。
现货储备快速准时交付常规储备量为6000+台,批量订单可快至当天发货,长期与品牌物流公司签约合作,可提供门对门的配送服务。
 现货储备快速准时交付
现货储备快速准时交付 常规储备量为6000+台,批量订单可快至当天发货,长期与品牌物流公司签约合作,可提供门对门的配送服务。
常规储备量为6000+台,批量订单可快至当天发货,长期与品牌物流公司签约合作,可提供门对门的配送服务。
 非标定制 满足个性需求微仪仪器拥有多年的测量试验设备制造经验 ,支持按实际应用需求,进行非标功能的开发定制,满足特定产品的试验需求。
非标定制 满足个性需求微仪仪器拥有多年的测量试验设备制造经验 ,支持按实际应用需求,进行非标功能的开发定制,满足特定产品的试验需求。
 非标定制 满足个性需求
非标定制 满足个性需求 微仪仪器拥有多年的光学显微镜制造经验 ,支持按实际应用需求,进行非标功能的开发定制,满足特定产品的试验需求。
微仪仪器拥有多年的光学显微镜制造经验 ,支持按实际应用需求,进行非标功能的开发定制,满足特定产品的试验需求。
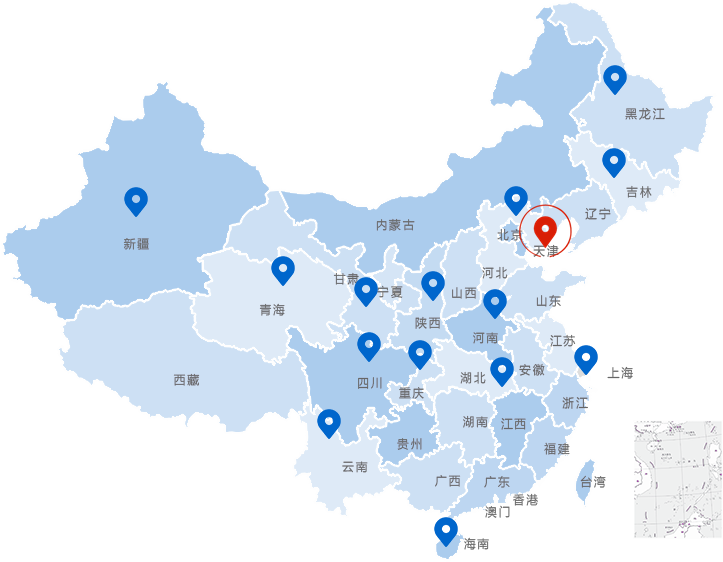
微仪仪器设有完善的服务体系,售后网络覆盖全国:天津、上海、北京、苏州、广东、重庆、成都、沈阳、哈尔滨、厦门、昆明、郑州等地,为全国用户提供更及时、更高效率的服务支持,提供更可靠的显微镜定制&解决方案。
 全国咨询热线:4001-123-022
全国咨询热线:4001-123-022
 需求分析requirement analysis
需求分析requirement analysis 推荐选型model selection
推荐选型model selection 设备调试Equipment debugging
设备调试Equipment debugging 操作培训Operation training
操作培训Operation training 技术援助technical assistance
技术援助technical assistance 售后服务after-sale service
售后服务after-sale service
给中实科技(天津)有限公司推荐使用我公司三目倒置荧光显微成像···【查看更多】
金相显微镜操作时的安全事项主要包括以下几个方面:一、基本操作···
恒信彩票金相显微镜在检测电路板(PCB板)时,主要遵循一系列严谨的操···
恒信彩票金相显微镜可视性不好可能由多种原因造成,以下是一些常见的解决···
恒信彩票金相显微镜在矿物学领域具有广泛的应用,为矿物学家提供了观察和···
友情链接:恒信彩票